Pin群

数学中，Pin 群是一个二次型空间相伴的克利福德代数的一个子群。它有一个到正交群的 2 对 1 映射，就像 Spin 群映到特殊正交群一样。

从 Pin 群到正交群的映射不是满的也不是万有覆叠空间，但对定二次型，两者都正确。

一般定义

确定形式

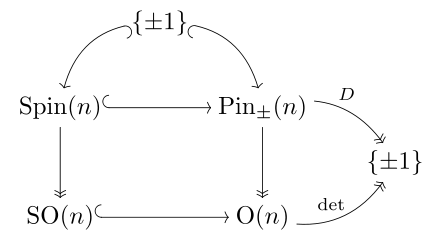
确定形式的 Pin 群是到正交群的满射，每个分支都是单连通的：它是正交群的二重覆叠。正定二次型 ${\displaystyle Q}$ 和它的负形式 ${\displaystyle -Q}$ 不是同构的，但是正交群是同构的 ^{[註 1]}。

就标准形式而言，${\displaystyle O(n,0)=O(0,n)}$，但是 ${\displaystyle {\mbox{Pin}}(n,0)\not \cong {\mbox{Pin}}(0,n)}$。使用 Clifford 代数（这里 ${\displaystyle v^{2}=Q(v)\in C\ell (V,Q)}$）中通用的“±”号记法，我们可以写成

${\displaystyle {\mbox{Pin}}_{+}(n):={\mbox{Pin}}(n,0)\qquad {\mbox{Pin}}_{-}(n):={\mbox{Pin}}(0,n)}$

它们都是到 ${\displaystyle O(n)=O(n,0)=O(0,n)}$ 的满射。

与之对比，我们有同构^{[註 2]} ${\displaystyle {\mbox{Spin}}(n,0)\cong {\mbox{Spin}}(0,n)}$ 且他们都是特殊正交群 SO(n) 惟一的万有覆叠。

不定形式

作为拓扑空间

任何连通拓扑群在拓扑意义上有惟一的万有覆叠空间，这个空间有惟一的群结构作为基本群的中心扩张。对一个不连通拓扑空间，含单位元的分支有一个惟一的万有覆叠，然后在其他分支作为拓扑空间可取同一个覆叠（这是单位分支的主齐性空间），但是其它分支的群结构一般不是惟一的。

Pin 和 Spin 群是和正交群和特殊正交群关联的独特的拓扑空间，由 Clifford 代数中得出：存在其他类似的群，对于于其他分支的其他二重覆叠或者其他群结构，但是他们不叫做 Pin 或 Spin 群，研究得也少。

结构

两个 Pin 群对应于中心扩张

${\displaystyle 1\to \{\pm 1\}\to {\mbox{Pin}}_{\pm }(V)\to O(V)\to 1}$

${\displaystyle {\mbox{Spin}}(V)}$（行列式为 1 的分支）上的群结构已经定义好了；其余分支的群结构由中心确定，从而有一个 ${\displaystyle \pm 1}$ 分歧。

两个扩张由一个反射的原像的平方是 ${\displaystyle \pm 1\in \ker \left({\mbox{Spin}}(V)\to SO(V)\right)}$ 区分，这两个 Pin 群即是这样命名的。明确地说，一个反射在 ${\displaystyle O(V)}$ 中的指数为 2，${\displaystyle r^{2}=1}$，所以反射的原像的平方（具有行列式 1）一定在 ${\displaystyle {\mbox{Spin}}_{\pm }(V)\to SO(V)}$ 的核中，所以 ${\displaystyle {\tilde {r}}^{2}=\pm 1}$，两种选择都确定了一个 Pin 群（因为所有反射共轭于联通群 ${\displaystyle SO(V)}$ 的中一个元素，所有反射的平方一定具有相同值）。

具体地，在 ${\displaystyle {\mbox{Pin}}_{+}}$ 中，${\displaystyle {\tilde {r}}}$ 的指数为 2，子群 ${\displaystyle \{1,r\}}$ 的原像是 ${\displaystyle C_{2}\times C_{2}}$：如果我们重复同一个反射，得到恒同。

在 ${\displaystyle {\mbox{Pin}}_{-}}$ 中，${\displaystyle {\tilde {r}}}$ 的指数为 4： 如果重复同一个反射两次，我们得到了一个“旋转 2π”——${\displaystyle {\mbox{Spin}}(V)\to SO(V)}$ 中的非平凡元可以理解为“旋转 2π”（每一个轴得出相同的元素）。

低维数

在 2 维，${\displaystyle {\mbox{Pin}}_{+}}$ 与 ${\displaystyle {\mbox{Pin}}_{-}}$ 的区别反映了一个正 2n 边形的二面体群和循环群 ${\displaystyle C_{2n}}$ 的区别。

在 ${\displaystyle {\mbox{Pin}}_{+}}$ 中，一个正 2n 边形的二面体群的原像，视为子群 ${\displaystyle {\mbox{Dih}}_{n}<O(2)}$，是 2n 边形的二面体群 ${\displaystyle {\mbox{Dih}}_{2n}<{\mbox{Pin}}_{+}(2)}$；然而在 ${\displaystyle {\mbox{Pin}}_{-}}$ 中二面体群的原像是循环群 ${\displaystyle {\mbox{Dic}}_{n}<{\mbox{Pin}}_{-}(2)}$

在 1维，Pin 群共轭于第一个二面体群和循环群：

${\displaystyle {\begin{aligned}{\mbox{Pin}}_{+}(1)&\cong C_{2}\times C_{2}={\mbox{Dih}}_{1}\\{\mbox{Pin}}_{-}(1)&\cong C_{4}={\mbox{Dic}}_{1}\end{aligned}}}$

中心

不定 Pin 群

Spin(p,q) 有八种不同的二重覆叠，对 ${\displaystyle p,q\neq 0}$，这对应于用 ${\displaystyle C_{2}}$ 中心扩张（中心不是 ${\displaystyle C_{2}\times C_{2}}$ 就是 ${\displaystyle C_{4}}$）。只有其中两个称为 Pin 群，他们可以将 Clifford 代数作为一个表示。他们分别称为 Pin(p,q) 和 Pin(q,p)。

命名

这个群的名称在 迈克尔·阿蒂亚、拉乌尔·博特、A. Shapiro： Clifford modules（Topology 3, suppl. 1 (1964), pp. 3-38, on page 3, line 17）一文中引入，他们说“这个笑话归于 J-P. Serre”。这是“Spin”的逆构词法：Pin 之于 Spin 就像 O(n) 之于 SO(n)，从而从“Spin”中去掉“S”得到“Pin”。进一步，词“Pin”的法语发音和一个粗痞话相同，这暗示了这个名称的起源于（或被归于）塞尔。^{[註 3]}

注释

参考文献