En funktion är inom matematisk analys en rationell funktion om, och endast om, den kan skrivas på formen

där m och n är naturliga tal och koefficienterna  kan vara reella eller komplexa tal. Koefficienterna kan tillhöra en godtycklig kropp K och i detta fall talar man om rationella funktioner och rationella bråk över K. Värdena kan tillhöra alla kroppar L innehållande K.
kan vara reella eller komplexa tal. Koefficienterna kan tillhöra en godtycklig kropp K och i detta fall talar man om rationella funktioner och rationella bråk över K. Värdena kan tillhöra alla kroppar L innehållande K.
Egenskaper
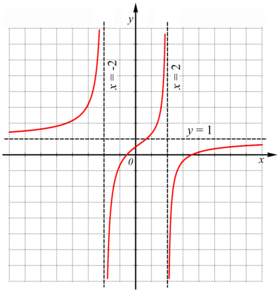
Figur 1: Den rationella funktionen

. Asymptoterna är linjer parallella med koordinatsystemets axlar
Figur 2: Den rationella funktionen

har den räta och icke axelparallella linjen

som asymptot, då täljarens grad är lika med nämnarens grad + 1
En rationell funktion (röd) och dess asymptoter. I detta fall finns en icke-linjär asymptot (grön)
Varje rationell funktion P(z)/Q(z) kan skrivas som ett icke-reducerbart bråk R(z) = P(z)/Q(z), där P(z) och Q(z) saknar gemensamma nollställen (är relativt prima).
Om P har graden m och Q har graden n, sägs graden av R(z) vara endera paret (m, n) eller talet m.
En rationell funktions största definitionsmängd är mängden av alla värden för vilka Qn är nollskild. En funktion som inte är rationell, det vill säga inte kan uttryckas som en kvot av två polynom, kallas irrationell funktion, en benämning som dock sällan används för funktioner.
Om Pm har ett högre gradtal än Qn kan den rationella funktionen skrivas på formen

där r har ett lägre gradtal än Q, vilket kan åstadkommas genom polynomdivision.
Det är möjligt att dela upp en rationell funktion i partialbråk. Om z är reellt eller komplext och P(z):s grad m är mindre än Q(z):s grad n och koefficienten för den högsta termen i Q(z) är 1, låt  vara ett nollställe till Q(z) av multiplicitet
vara ett nollställe till Q(z) av multiplicitet  och där
och där  så att
så att

Den rationella funktionen P(z)/Q(z) kan då unikt representeras på formen

där  är termer som återstår att bestämma.
är termer som återstår att bestämma.
Exempel
Den rationella funktion, som i sina huvuddrag avbildas i figur 2,

är odefinierad för värdena  och den är asymptotisk till
och den är asymptotisk till  när x går mot oändligheten.
när x går mot oändligheten.
Den rationella funktionen  är definierad för alla reella tal, men inte för alla komplexa tal, därför att om x är den imaginära enheten, leder en beräkning till division med noll:
är definierad för alla reella tal, men inte för alla komplexa tal, därför att om x är den imaginära enheten, leder en beräkning till division med noll:
 ,
,
vilket är odefinierat.
Asymptoter
Vid undersökning av en rationell funktion är, förutom derivatans nollställen, även nämnarens nollställen intressanta, eftersom nämnaren måste vara nollskild.
Det finns tre fall att undersöka med utgångspunkt i täljarens respektive nämnarens gradtal:

- Funktionen har asymptoten x = a om
 och vågräta asymptoter i de punkter där derivatan går mot noll.
och vågräta asymptoter i de punkter där derivatan går mot noll. - Att hitta den vågräta asymptoten görs enklast genom att dividera med termen med högst gradtal i både täljare och nämnare och låta
 .
.

- Funktionen har de lodräta asymptoterna
 om
om  och den vågräta asymptoten
och den vågräta asymptoten  där c är en konstant.
där c är en konstant. - Även här förlängs bråket med 1 delat med högstagradstermen i både täljare och nämnare för att sedan låta
 .
.

- De lodräta asymptoterna erhålls som tidigare genom att sätta nämnaren till noll. I det fall då
 förekommer en asymptot, vilken inte är axelparallell, (linjen
förekommer en asymptot, vilken inte är axelparallell, (linjen  ). Denna asymptots ekvation bestäms enklast genom polynomdivision av
). Denna asymptots ekvation bestäms enklast genom polynomdivision av  med
med  och sedan låta
och sedan låta  →
→  .
.
Exempel
Med användning av exemplet i figur 1:

De lodräta asymptoterna är linjerna som svarar mot nämnarens nollställen: 
De vågräta asymtoterna kan bestämmas genom att låta x gå mot oändligheten. Dividera med högstagradstermen i både täljare och nämnare:

Den vågräta asymptoten är alltså y = 1.
Det går också att använda polynomdivision, vilket ger likheten

När x går mot oändligheten går y mot

och den vågräta asymptoten är således y = 1
Rationella funktioner som integrander
Till skillnad från de polynom på vilka rationella funktioner bygger, är det ofta ganska svårt att hitta primitiva funktioner då integranden är en rationell funktion. För integrering av rationella funktioner krävs ofta transformationer eller utnyttjande av kända integraler, vilket kan kräva omvandling av integranden till någon eller några av dessa kända former. Exempel på sådana integraler:


 eller
eller 



Exempel
Bestäm integralen av

Efter polynomdivision kan f skrivas
 .
.
Genom att tillämpa den första regeln är en möjlig primitiv funktion

Användning
Inom komplex analys ses rationella funktioner som avbildningar inom riemannsfären och specialfallet då båda polynomen i funktionen är linjära kallas Möbiusavbildning.
Inom abstrakt algebra är mängden av alla rationella funktioner över en kropp fraktionskroppen till polynomringen över kroppen.
Källor
- Hazewinkel, Michiel, red. (2001), ”Rational function”, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104