Processo di nascita e morte

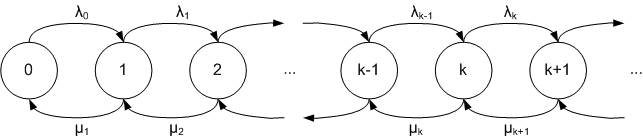
Un processo di nascita e morte è un processo stocastico markoviano a tempo continuo sullo spazio degli stati dato dall'insieme dei numeri naturali, che simula l'andamento di una popolazione i cui unici cambiamenti siano le nascite e le morti. In altre parole, se il processo si trova in uno stato n, può solamente passare o allo stato n+1 (nascita) o allo stato n-1 (morte). I processi di nascita e morte hanno importanti applicazioni in biologia, teoria delle code e demografia.

Un processo di nascita e morte è un processo stocastico su ${\displaystyle \mathbb {N} }$ che soddisfa le seguenti proprietà:

• Gli incrementi sono indipendenti, ossia la quantità di passaggi di stato in intervalli disgiunti sono indipendenti tra loro.
• Se il processo si trova in n, la probabilità di una nascita in un piccolo intervallo di tempo è proporzionale alla lunghezza dell'intervallo, ossia per ${\displaystyle h\to 0}$

${\displaystyle \mathbb {P} (N_{t+h}-N_{t}=1)=\lambda _{n}h+o(h).}$

• Se il processo si trova in n>0, la probabilità di una morte in un piccolo intervallo di tempo è proporzionale alla lunghezza dell'intervallo, ossia per ${\displaystyle h\to 0}$

${\displaystyle \mathbb {P} (N_{t+h}-N_{t}=-1)=\mu _{n}h+o(h).}$

• Se il processo si trova in n, la probabilità che il processo si allontani per più di due stati è trascurabile, ossia per ${\displaystyle h\rightarrow 0}$

${\displaystyle \mathbb {P} (|N_{t+h}-N_{t}|\geq 2)=o(h).}$

Le quantità λ_n e μ_n sono i coefficienti di natalità e di mortalità.

• Il processo soddisfa la proprietà di Markov.
• Il processo soddisfa la proprietà di Markov forte.
• La probabilità che il processo resti nello stesso stato in un piccolo intervallo di tempo è data, per ${\displaystyle h\rightarrow 0}$, da

${\displaystyle \mathbb {P} (N_{t+h}-N_{t}=0)=1-(\mu _{n}+\lambda _{n})h+o(h).}$

• Il tempo di attesa tra un passaggio di stato e il successivo ha legge esponenziale di parametro (λ_n + μ_n).
• Il processo di Poisson è un caso particolare di processo di nascita e morte nel caso in cui μ_n=0 e λ_n=λ per ogni n.

Le condizioni per la ricorrenza e la transitorietà sono state stabilite da Samuel Karlin e James McGregor.^[1].

Un processo di nascita e morte è ricorrente se e solo se

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty .}$

Un processo di nascita e morte è ergodico se e solo se

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{e}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}<\infty .}$

Un processo di nascita e morte è nullo-ricorrente se e solo se

${\displaystyle \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{e}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}=\infty .}$

Le condizioni per la ricorrenza, la transitorietà, l'ergodicità e la ricorrenza nulla possono essere derivate in una forma più esplicita^[2].

Per ogni intero ${\displaystyle K\geq 1}$, sia ${\displaystyle \ln _{(K)}(x)}$ la ${\displaystyle K}$-esima iterazione del logaritmo naturale, ossia ${\displaystyle \ln _{(1)}(x)=\ln(x)}$, e per qualsiasi ${\displaystyle 2\leq k\leq K}$, ${\displaystyle \ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))}$.

Quindi, le condizioni per la ricorrenza e la transitorietà di un processo di nascita e morte sono le seguenti.

Il processo di nascita e morte è transitorio se esistono ${\displaystyle c>1}$, ${\displaystyle K\geq 1}$ e ${\displaystyle n_{0}}$, tale che per ogni ${\displaystyle n>n_{0}}$ si ha

${\displaystyle {\frac {\lambda _{n}}{\mu _{n}}}\geq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K-1}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}+{\frac {c}{n\prod _{j=1}^{K}\ln _{(j)}(n)}},}$

dove la somma vuota per ${\displaystyle K=1}$ si assume che sia 0.

Il processo di nascita e morte è ricorrente se esistono ${\displaystyle K\geq 1}$ e ${\displaystyle n_{0}}$, tali che per ogni ${\displaystyle n>n_{0}}$ si ha

${\displaystyle {\frac {\lambda _{n}}{\mu _{n}}}\leq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}.}$

Possono essere trovate classi più ampie di processi di nascita e morte per i quali è possibile stabilire le condizioni per la ricorrenza e la transitorietà^[3].

Consideriamo il passeggiata aleatoria unidimensionale ${\displaystyle S_{t}}$, ${\displaystyle t=0,1,\ldots }$, che è definito come segue. Lasciare ${\displaystyle S_{0}=1}$ e ${\displaystyle S_{t}=S_{t-1}+e_{t}}$, ${\displaystyle t\geq 1}$, dove ${\displaystyle e_{t}}$ accetta valori ${\displaystyle \pm 1}$, e la distribuzione di ${\displaystyle S(t)}$ è definito dalle seguenti condizioni:

${\displaystyle \mathbb {P} \{S_{t+1}=S_{t}+1|S_{t}>0\}={\frac {1}{2}}+{\frac {\alpha _{S_{t}}}{S_{t}}},\quad \mathbb {P} \{S_{t+1}=S_{t}-1|S_{t}>0\}={\frac {1}{2}}-{\frac {\alpha _{S_{t}}}{S_{t}}},\quad \mathbb {P} \{S_{t+1}=1|S_{t}=0\}=1,}$

dove ${\displaystyle \alpha _{n}}$ soddisfano la condizione ${\displaystyle 0<\alpha _{n}<\min\{C,n/2\}}$, ${\displaystyle C>0}$.

Il passeggiata aleatoria qui descritto è un analogo a tempo discreto del processo di nascita e morte (vedi catena di Markov) con i tassi di natalità

${\displaystyle {\frac {1}{2}}+{\frac {\alpha _{n}}{2}},}$

e i tassi di mortalità

${\displaystyle {\frac {1}{2}}-{\frac {\alpha _{n}}{2}}.}$

Quindi, la ricorrenza o la transitorietà del passeggiata aleatoria è associata alla ricorrenza o alla transitorietà del processo di nascita e morte.^[2]

La passeggiata aleatoria è transitorio se esiste ${\displaystyle c>1}$, ${\displaystyle K\geq 1}$ e ${\displaystyle n_{0}}$ tale che per ogni ${\displaystyle n>n_{0}}$

${\displaystyle \alpha _{n}\geq {\frac {1}{4}}\left(1+\sum _{k=1}^{K-1}\prod _{j=1}^{k}{\frac {1}{\ln _{(j)}(n)}}+c\prod _{j=1}^{K}{\frac {1}{\ln _{(j)}(n)}}\right),}$

dove la somma vuota per ${\displaystyle K=1}$ è assunto pari a zero.

La passeggiata aleatoria è ricorrente se esiste ${\displaystyle K\geq 1}$ e ${\displaystyle n_{0}}$ tale che per ogni ${\displaystyle n>n_{0}}$

${\displaystyle \alpha _{n}\leq \left(1+\sum _{k=1}^{K}\prod _{j=1}^{k}{\frac {1}{\ln _{(j)}(n)}}\right).}$

• Samuel Karlin e Howard M. Taylor, A first course in stochastic processes, Academic Press, 1975.

• Teoria delle code
• Processo stocastico
• Processo markoviano

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica