Distribuzione logistica

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

Distribuzione logistica
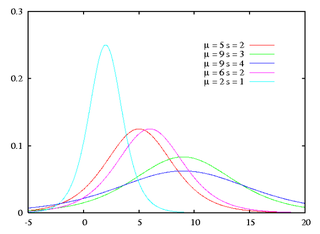
Funzione di densità di probabilità
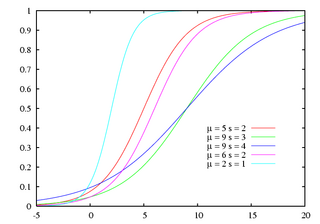
Funzione di ripartizione
Parametri	${\displaystyle \mu }$ (media) ${\displaystyle s>0\ }$
Supporto	${\displaystyle \mathbb {R} }$
Funzione di densità	${\displaystyle {\frac {e^{-{\frac {x-\mu }{s}}}}{s\left(1+e^{-{\frac {x-\mu }{s}}}\right)^{2}}}}$
Funzione di ripartizione	${\displaystyle {\frac {1}{1+e^{-{\frac {x-\mu }{s}}}}}}$
Valore atteso	${\displaystyle \mu \ }$
Mediana	${\displaystyle \mu \ }$
Moda	${\displaystyle \mu \ }$
Varianza	${\displaystyle {\frac {\pi ^{2}}{3}}s^{2}}$
Indice di asimmetria	${\displaystyle 0\ }$
Curtosi	${\displaystyle {\frac {6}{5}}}$
Entropia	${\displaystyle 2+\log s\ }$
Funzione generatrice dei momenti	${\displaystyle e^{\mu t}\mathrm {B} (1-st,1+st)\ }$ (con ${\displaystyle \mathrm {B} }$ la funzione Beta, definita per ${\displaystyle st}$ con parte reale compresa tra -1 e 1)
Funzione caratteristica	${\displaystyle e^{i\mu t}\mathrm {B} (1-ist,1+ist)\ }$ (con ${\displaystyle \mathrm {B} }$ la funzione Beta, definita per ${\displaystyle ist}$ con parte reale compresa tra -1 e 1)
Manuale

In teoria delle probabilità la distribuzione logistica è una distribuzione di probabilità continua definita sui numeri reali e legata all'equazione logistica descritta dal matematico belga Pierre François Verhulst.

Viene utilizzata in molti degli ambiti che descrivono modelli di crescita tramite l'equazione logistica.

Definizione

La distribuzione logistica è una distribuzione di probabilità la cui funzione di ripartizione risolve l'equazione logistica

${\displaystyle F'={\frac {1}{s}}F(1-F),}$

con ${\displaystyle s>0.}$

La distribuzione logistica di parametri ${\displaystyle (s,\mu )}$ ha funzione di ripartizione

${\displaystyle F(x)={\frac {1}{1+e^{-{\frac {x-\mu }{s}}}}},}$

e funzione di densità di probabilità

${\displaystyle f(x)=F'(x)={\frac {e^{-{\frac {x-\mu }{s}}}}{s\left(1+e^{-{\frac {x-\mu }{s}}}\right)^{2}}}.}$

Le due funzioni possono anche essere espresse in termini di funzioni iperboliche come

${\displaystyle f(x)={\tfrac {1}{4s}}(\cosh {\tfrac {x-\mu }{2s}})^{-2},}$

${\displaystyle F(x)={\tfrac {1}{2}}+{\tfrac {1}{2}}\tanh {\tfrac {x-\mu }{2s}},}$

dove ${\displaystyle \cosh(t)={\tfrac {e^{t}+e^{-t}}{2}}}$ è il coseno iperbolico e ${\displaystyle \tanh(t)={\tfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$ la tangente iperbolica.

Caratteristiche

La distribuzione logistica di parametri ${\displaystyle (s,\mu )}$ ha densità di probabilità simmetrica rispetto a ${\displaystyle \mu }$, dove assume il valore massimo. In particolare ha speranza matematica, mediana e moda pari a ${\displaystyle \mu }$, mentre il suo indice di asimmetria è ${\displaystyle 0.}$

I quantili ${\displaystyle q_{\alpha }}$ di ordine ${\displaystyle \alpha }$ possono essere determinati tramite l'inversa della funzione di ripartizione,

${\displaystyle q_{\alpha }=F^{-1}(\alpha )=\mu +s\log {\tfrac {\alpha }{1-\alpha }}.}$

La funzione ${\displaystyle \log {\tfrac {x}{1-x}}}$ è detta funzione logit.

I momenti centrali della distribuzione sono

${\displaystyle m_{k}=\int _{\mathbb {R} }(x-\mu )^{k}f(x)dx=\int _{\mathbb {R} }(x-\mu )^{k}dF(x)=\int _{0}^{1}\left(s\log {\tfrac {t}{1-t}}\right)^{k}dt=s^{k}\pi ^{k}(2^{k}-2)|B_{k}|,}$

dove ${\displaystyle B_{k}}$ è il ${\displaystyle k}$-esimo numero di Bernoulli.

In particolare la distribuzione ha varianza ${\displaystyle {\frac {\pi ^{2}}{3}}s^{2}}$ e coefficiente di curtosi ${\displaystyle \gamma _{2}={\frac {6}{5}}.}$

Altre distribuzioni

La distribuzione log-logistica (o loglogistica) è la distribuzione di probabilità di una variabile aleatoria ${\displaystyle X}$ il cui logaritmo ${\displaystyle \log X}$ segua la distribuzione logistica.

Voci correlate

• Equazione logistica

Altri progetti

• Wikimedia Commons contiene immagini o altri file su distribuzione logistica

Collegamenti esterni

• (EN) Eric W. Weisstein, Distribuzione logistica, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica