Kúp

A matematikában a kúp (idegen szóval kónusz) gúlaszerű térbeli test. A kúp alapja egy tetszőleges síkidom, palástját a csúcsot az alap határpontjaival összekötő egyenes szakaszok, az alkotók uniója alkotja. Megkülönböztethetünk egyenes és ferde kúpokat aszerint, hogy a csúcs merőleges vetülete az alapra egybeesik-e az alap középpontjával, ha utóbbi értelmezett. Kúp alatt leggyakrabban az egyenes, kör alapú kúpokat értik. A kúpot az alapjával párhuzamos síkkal elmetszve csonkakúpot kapunk.

Képletek

A kúpoknak létezik térfogata és felszíne.^[1]

Térfogat

Jelölje ${\displaystyle b}$ a kúp alapjának a területét, s legyen ${\displaystyle h}$ a magassága. Ekkor a térfogat az alábbiak szerint számítható:

${\displaystyle V={\frac {1}{3}}bh}$

Speciálisan, ha a kúp kör alapú, akkor ${\displaystyle r}$-rel jelölve a kör sugarát, így részletezhető a formula:

${\displaystyle V={\frac {1}{3}}\pi r^{2}h}$

A másik esetben, ha az alap elliptikus, akkor pedig az ellipszis sugarait ${\displaystyle r_{1}}$ és ${\displaystyle r_{2}}$ szimbólumokkal jelölve a következőképpen:

${\displaystyle V={\frac {1}{3}}\pi r_{1}r_{2}h}$

Felszín

A kúp felszíne az alap és a palást területének összege. Az egyenes, köralapú kúp esetében erre adható egyszerű képlet:

${\displaystyle A=\pi r^{2}+\pi ra}$

ahol ${\displaystyle a}$ a kúp egy alkotójának hossza, képlete:

${\displaystyle a={\sqrt {r^{2}+h^{2}}}}$

Ez a Pitagorasz-tétel egyenes következménye.

Beírható gömb sugara

Az egyenes körkúpba írható gömb ρ sugarának képlete:

${\displaystyle \rho ={\frac {3V}{A}}}$

ahol A jelöli a kúp felszínét, V pedig a térfogatát.^[2]

Egyenletek

A ${\displaystyle h}$ magasságú és ${\displaystyle \vartheta }$ fél nyílásszögű kúp, aminek forgástengelye a ${\displaystyle z}$ tengely, csúcsa az origó, így paraméterezhető:

${\displaystyle S(s,t,u)=\left(u\mathrm {tg} s\cos t,u\mathrm {tg} s\sin t,u\right)}$

ahol ${\displaystyle s,t,u}$ rendre a ${\displaystyle [0,\vartheta )}$, ${\displaystyle [0,2\pi )}$, és ${\displaystyle [0,h]}$ intervallumokba esik.

Ugyanez a test implicit az

${\displaystyle \{S(x,y,z)\leq 0,z\geq 0,z\leq h\}}$

egyenlőtlenségekkel adható meg, ahol

${\displaystyle S(x,y,z)=(x^{2}+y^{2})(\cos \vartheta )^{2}-z^{2}(\sin \vartheta )^{2}.\,}$

Általánosabban a ${\displaystyle d}$ vektorral párhuzamos forgástengelyű origó csúcsú körkúp, aminek fél nyílásszöge ${\displaystyle \vartheta }$ az ${\displaystyle S(u)=0}$ vektoregyenlettel adható meg, ahol

${\displaystyle S(u)=(u\cdot d)^{2}-(d\cdot d)(u\cdot u)(\cos \vartheta )^{2}}$   vagy   ${\displaystyle S(u)=u\cdot d-|d||u|\cos \vartheta }$

ahol ${\displaystyle u=(x,y,z)}$, és ${\displaystyle u\cdot d}$ skalárszorzat.

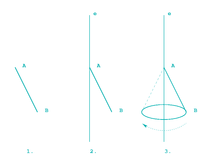
Az egyenes körkúp mint forgástest

Az egyenes körkúp forgástestként is generálható egy AB szakaszt elforgatva annak pontosan egy végpontján áthaladó egyenes körül. Ebben az esetben az AB szakaszt nevezik a kúp alkotójának is. Ekkor fennáll az alábbi egyenlőség:

${\displaystyle |AB|^{2}=h^{2}+r^{2}\,}$

Lineáris algebra

A lineáris algebrában vektorok egy halmaza kúp, ha zárt a nemnegatív számmal való szorzásra.

Egy kúp végesen generált, ha minden pontja előáll véges sok vektor lineáris kombinációjaként. Egy kúp metszetkúp, ha előáll véges sok féltér metszeteként. Ebből azonnal következik, hogy metszetkúp mindig konvex. Megmutatható, hogy metszetkúp mindig generált kúp, továbbá ha egy végesen generált kúp konvex, akkor metszetkúp.

A térfogat- és felszínképletek bizonyítása

Térfogat

Az elemi geometriában gyakran a Cavalieri-elvet használják: veszünk egy ugyanakkora alapterületű és magasságú gúlát. Az alappal párhuzamosan szeletelve a két testet középpontos hasonlósággal adódik, hogy az ugyanolyan magasságú szeletek területe egyenlő. Ezért a két test térfogata egyenlő.

A T alapterületű és h magasságú gúla térfogata

${\displaystyle V={\frac {1}{3}}\cdot T\cdot h}$

Ez alapján a kúp térfogata

${\displaystyle V={\frac {1}{3}}\cdot r^{2}\cdot \pi \cdot h}$.

A kúp alapterülete növekvő oldalszámú sokszögekkel is közelíthető.

Egy másik bizonyítás az integrálszámítást hívja segítségül. A derékszögű koordináta-rendszerben a kúp csúcsát az origóba, és az alapkör középpontját a (h,0) pontba teszi. Ezután a kúpot, mint végtelen sok lapos, dx magasságú hengerből összetett forgástestet tekinti. A párhuzamos szelők tételével:

Egy infinitezimális henger sugara:

${\displaystyle r_{Z}(h)={\frac {r}{h}}\cdot x}$

Egy infinitezimális henger térfogata:

${\displaystyle \left({\frac {r}{h}}\cdot x\right)^{2}\cdot \pi \cdot dx={\frac {r^{2}}{h^{2}}}\cdot \pi \cdot x^{2}\,dx}$

A forgáskúp térfogata megegyezik ezeknek a hengereknek a térfogatösszegével. Ezt határozott integrállal számítja ki, ahol a határok 0 és h:

${\displaystyle V=\int _{0}^{h}{\frac {r^{2}}{h^{2}}}\cdot \pi \cdot x^{2}\,dx={\frac {r^{2}\cdot \pi }{h^{2}}}\cdot \int _{0}^{h}x^{2}\,dx}$

${\displaystyle V={\frac {r^{2}\cdot \pi }{h^{2}}}\cdot \left[{\frac {x^{3}}{3}}\right]_{0}^{h}}$

${\displaystyle V={\frac {r^{2}\cdot \pi }{h^{2}}}\cdot \left({\frac {h^{3}}{3}}-{\frac {0^{3}}{3}}\right)}$

${\displaystyle V={\frac {r^{2}\cdot \pi }{h^{2}}}\cdot {\frac {h^{3}}{3}}}$

Így jut az ismert

${\displaystyle V={\frac {r^{2}\cdot \pi \cdot h}{3}}={\frac {1}{3}}\cdot r^{2}\cdot \pi \cdot h}$

képlethez.

A kúppalást felszíne

Az egyenes körkúp palástja görbült, de kiteríthető körcikké. Ennek sugara megegyezik a kúp alkotójának hosszával (a). A körcikk α középponti szöge arányegyenlettel számítható: a középponti szög úgy aránylik a teljesszöghöz, mint az alapkör 2πr kerülete az a sugarú kör teljes kerületéhez:

${\displaystyle \alpha :360^{\circ }=(2\pi r):(2\pi a)=r:a}$

ahol ${\displaystyle a={\sqrt {r^{2}+h^{2}}}}$ a kúp alkotója és a körcikk sugara.

A kúppalást felszíne eszerint a körcikk területképletéből adódóan

${\displaystyle A_{P}={\frac {\alpha }{360^{\circ }}}\cdot a^{2}\cdot \pi ={\frac {r}{a}}\cdot a^{2}\cdot \pi =ra\pi }$

Jegyzetek

Források

• Frank András: Operációkutatás
• Spinning Cone from Math Is Fun
• Paper model cone
• Lateral surface area of an oblique cone
• Generalized Cone from Wolfram MathWorld

Külső hivatkozások

• Weisstein, Eric W.: Kúp (angol nyelven). Wolfram MathWorld
• Weisstein, Eric W.: Csonkakúp (angol nyelven). Wolfram MathWorld