Signal sinusoïdal

Signal sinusoïdal simple.

Un signal sinusoïdal est un signal continu (onde) dont l’amplitude, observée à un endroit précis, est une fonction sinusoïdale du temps, définie à partir de la fonction sinus.

La courbe associée s'appelle une sinusoïde (voir Figure 1).

Caractéristiques d'un signal sinusoïdal

Un signal sinusoïdal est caractérisé par son amplitude maximale et sa fréquence. Il peut s'écrire sous la forme :

s ( t ) = A sin ⁡ ( ω t + φ ) {\displaystyle s(t)=A\,\sin(\omega t+\varphi )\,}

avec :

A : amplitude de la grandeur, appelée aussi valeur de crête, dans l'unité de la grandeur mesurée
ω : pulsation de la grandeur en rad s−1
ω t + φ : phase instantanée en rad
φ : phase à l'origine en rad (souvent fixée par l'expérimentateur)

La pulsation, la fréquence et la période sont liées par les relations :

ω = 2 π f = 2 π T {\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}

Lorsque l'on compare deux signaux de même fréquence, il est nécessaire d’indiquer de combien de temps ils sont décalés. Les signaux sont « en phase » s'ils sont superposés, sinon il y a un déphasage.

  • Signaux déphasés de 90°, dits « en quadrature de phase ».
    Signaux déphasés de 90°, dits « en quadrature de phase ».
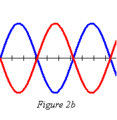  • Signaux déphasés de 180°, dits « en opposition de phase ».
    Signaux déphasés de 180°, dits « en opposition de phase ».

Le déphasage se déduit par une simple règle de 3 du décalage temporel séparant les deux signaux.

En effet, 0° (ou 0 radian) correspond à 0 seconde de déphasage et 360° (ou 2π radians) correspondent à des signaux décalés d’une période (T), ils sont alors à nouveau en phase. Si on appelle τ le décalage temporel entre les signaux, on peut écrire :

en degrés : Δ φ = τ ⋅ 360 T {\displaystyle \Delta \varphi =\tau \cdot {\frac {360}{T}}}
en radians : Δ φ = τ ⋅ 2 π T {\displaystyle \Delta \varphi =\tau \cdot {\frac {2\pi }{T}}}

Exemples

L’amplitude du signal peut correspondre à une pression (son), à un déplacement (corde qui vibre), à une quantité d’électrons en déplacement (courant électrique) ou encore à une onde électromagnétique.

L'importance des signaux sinusoïdaux est encore accrue par les résultats issus de l'analyse harmonique, qui exploite le fait que toute grandeur périodique peut se décomposer en somme de termes sinusoïdaux à l'aide de la décomposition en séries de Fourier.

Opérations arithmétiques avec les grandeurs sinusoïdales

Afin de réaliser les opérations d'addition ou de soustraction de grandeurs sinusoïdales, on utilise la représentation de Fresnel ou la transformation complexe.

Voir aussi

Sur les autres projets Wikimedia :

  • sinusoïdal, sur le Wiktionnaire

Articles connexes

Lien externe

  • Robert Ferréol, « Sinusoïde », sur Encyclopédie des formes mathématiques remarquables
v · m
Traitement du signal
Théorie
Techniques
Domaines d'applications
Signaux
  • icône décorative Portail de la physique