Planar SAT

In computer science, the planar 3-satisfiability problem (abbreviated PLANAR 3SAT or PL3SAT) is an extension of the classical Boolean 3-satisfiability problem to a planar incidence graph. In other words, it asks whether the variables of a given Boolean formula—whose incidence graph consisting of variables and clauses can be embedded on a plane—can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

Like 3SAT, PLANAR-SAT is NP-complete, and is commonly used in reductions.

Definition

Every 3SAT problem can be converted to an incidence graph in the following manner: For every variable ${\displaystyle v_{i}}$, the graph has one corresponding node ${\displaystyle v_{i}}$, and for every clause ${\displaystyle c_{j}}$, the graph has one corresponding node ${\displaystyle c_{j}.}$ An edge ${\displaystyle (v_{i},c_{j})}$ is created between variable ${\displaystyle v_{i}}$ and clause ${\displaystyle c_{j}}$ whenever ${\displaystyle v_{i}}$ or ${\displaystyle \lnot v_{i}}$ is in ${\displaystyle c_{j}}$. Positive and negative literals are distinguished using edge colorings.

The formula is satisfiable if and only if there is a way to assign TRUE or FALSE to each variable node such that every clause node is connected to at least one TRUE by a positive edge or FALSE by a negative edge.

A planar graph is a graph that can be drawn on the plane in a way such that no two of its edges cross each other. Planar 3SAT is a subset of 3SAT in which the incidence graph of the variables and clauses of a Boolean formula is planar. It is important because it is a restricted variant, and is still NP-complete. Many problems (for example games and puzzles) cannot represent non-planar graphs. Hence, Planar 3SAT provides a way to prove those problems to be NP-hard.

Proof of NP-completeness

The following proof sketch follows the proof of D. Lichtenstein.^[1]

Trivially, PLANAR 3SAT is in NP. It is thus sufficient to show that it is NP-hard via reduction from 3SAT.

This proof makes use of the fact that ${\displaystyle (\lnot a\lor \lnot b\lor c)\land (a\lor \lnot c)\land (b\lor \lnot c)}$ is equivalent to ${\displaystyle (a\land b)\leftrightarrow c}$ and that ${\displaystyle (a\lor \lnot b)\land (\lnot a\lor b)}$ is equivalent to ${\displaystyle a\leftrightarrow b}$.

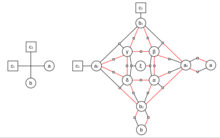
First, draw the incidence graph of the 3SAT formula. Since no two variables or clauses are connected, the resulting graph will be bipartite. Suppose the resulting graph is not planar. For every crossing of edges (a, c₁) and (b, c₂), introduce nine new variables a₁, b₁, α, β, γ, δ, ξ, a₂, b₂, and replace every crossing of edges with a crossover gadget shown in the diagram. It consists of the following new clauses:

$${\displaystyle {\begin{array}{ll}(\lnot a_{2}\lor \lnot b_{2}\lor \alpha )\land (a_{2}\lor \lnot \alpha )\land (b_{2}\lor \lnot \alpha ),&\quad {\text{i.e.,}}\quad a_{2}\land b_{2}\leftrightarrow \alpha \\(\lnot a_{2}\lor b_{1}\lor \beta )\land (a_{2}\lor \lnot \beta )\land (\lnot b_{1}\lor \lnot \beta ),&\quad {\text{i.e.,}}\quad a_{2}\land \lnot b_{1}\leftrightarrow \beta \\(a_{1}\lor b_{1}\lor \gamma )\land (\lnot a_{1}\lor \lnot \gamma )\land (\lnot b_{1}\lor \lnot \gamma ),&\quad {\text{i.e.,}}\quad \lnot a_{1}\land \lnot b_{1}\leftrightarrow \gamma \\(a_{1}\lor \lnot b_{2}\lor \delta )\land (\lnot a_{1}\lor \lnot \delta )\land (b_{2}\lor \lnot \delta ),&\quad {\text{i.e.,}}\quad \lnot a_{1}\land b_{2}\leftrightarrow \delta \\(\alpha \lor \beta \lor \xi )\land (\gamma \lor \delta \lor \lnot \xi ),&\quad {\text{i.e.,}}\quad \alpha \lor \beta \lor \gamma \lor \delta \\(\lnot \alpha \lor \lnot \beta )\land (\lnot \beta \lor \lnot \gamma )\land (\lnot \gamma \lor \lnot \delta )\land (\lnot \delta \lor \lnot \alpha ),&\\(a_{2}\lor \lnot a)\land (a\lor \lnot a_{2})\land (b_{2}\lor \lnot b)\land (b\lor \lnot b_{2}),&\quad {\text{i.e.,}}\quad a\leftrightarrow a_{2},~b\leftrightarrow b_{2}\\\end{array}}}$$

If the edge (a, c₁) is inverted in the original graph, (a₁, c₁) should be inverted in the crossover gadget. Similarly if the edge (b, c₂) is inverted in the original, (b₁, c₂) should be inverted.

One can easily show that these clauses are satisfiable if and only if ${\displaystyle a\leftrightarrow a_{1}}$ and ${\displaystyle b\leftrightarrow b_{1}}$.

This algorithm shows that it is possible to convert each crossing into its planar equivalent using only a constant amount of new additions. Since the number of crossings is polynomial in terms of the number of clauses and variables, the reduction is polynomial.^[2]

Variants and related problems

• Planar 3SAT with a variable-cycle: Here, in addition to the incidence-graph, the graph also includes a cycle going through all the variables, and each clause is either inside or outside this cycle. The resulting graph must still be planar. This problem is NP-complete.^[1]
  • However, if the problem is further restricted such that all clauses are inside the variable-cycle, or all clauses are outside it, then the problem can be solved in polynomial time using dynamic programming.
• Planar 3SAT with literals: The bipartite incidence graph of the literals and clauses is planar too. This problem is NP-complete.^[1]
• Planar rectilinear 3SAT: Vertices of the graph are represented as horizontal segments. Each variable lies on the x-axis while each clause lies above/below the x-axis. Every connection between a variable and a clause must be a vertical segment. Each clause may only have up to 3 connections with variables and are either all-positive or all-negative. This problem is NP-complete.^[3]
  • Planar monotone rectilinear 3SAT: This is a variant of planar rectilinear 3SAT where the clauses above the x-axis are all-positive and the clauses below the x-axis are all-negative. This problem is NP-complete^[4] and remains NP-complete when each clause containing three variables has two neighboring variables that are adjacent on the x-axis (i.e., no other variable appears horizontally between the neighboring variables).^[5]
• Planar 1-in-3SAT: This is the planar equivalent of 1-in-3SAT. It is NP-complete.^[6]
  • Planar positive rectilinear 1-in-3SAT: This is the planar equivalent of positive 1-in-3SAT. It is NP-complete.^[7]
• Planar NAE 3SAT: This problem is the planar equivalent of NAE 3SAT. Unlike the other variants, this problem can be solved in polynomial time. The proof is by reduction to planar maximum cut.^[8]
• Planar circuit SAT: This is a variant of circuit SAT in which the circuit, computing the SAT formula, is a planar directed acyclic graph. Note that this is a different graph than the adjacency graph of the formula. This problem is NP-complete.^[9]

Reductions

Logic puzzles

Reduction from Planar SAT is a commonly used method in NP-completeness proofs of logic puzzles. Examples of these include Fillomino,^[10] Nurikabe,^[11] Shakashaka,^[12] Tatamibari,^[13] and Tentai Show.^[14] These proofs involve constructing gadgets that can simulate wires carrying signals (Boolean values), input and output gates, signal splitters, NOT gates and AND (or OR) gates in order to represent the planar embedding of any Boolean circuit. Since the circuits are planar, crossover of wires do not need to be considered.

Flat folding of fixed-angle chains

This is the problem of deciding whether a polygonal chain with fixed edge lengths and angles has a planar configuration without crossings. It has been proven to be strongly NP-hard via a reduction from planar monotone rectilinear 3SAT.^[15]

Minimum edge-length partition

This is the problem of partitioning a polygon into simpler polygons such that the total length of all edges used in the partition is as small as possible.

When the figure is a rectilinear polygon and it should be partitioned into rectangles, and the polygon is hole-free, then the problem is polynomial. But if it contains holes (even degenerate holes—single points), the problem is NP-hard, by reduction from Planar SAT. The same holds if the figure is any polygon and it should be partitioned into convex figures.^[16]

A related problem is minimum-weight triangulation - finding a triangulation of minimal total edge length. The decision version of this problem is proven to be NP-complete via a reduction from a variant of Planar 1-in-3SAT.^[17]

References