Implication graph

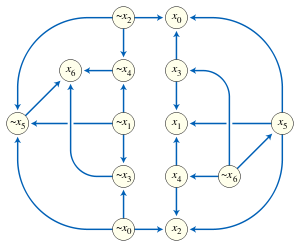
In mathematical logic and graph theory, an implication graph is a skew-symmetric, directed graph G = (V, E) composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal u is true then the literal v is also true". Implication graphs were originally used for analyzing complex Boolean expressions.

Applications

A 2-satisfiability instance in conjunctive normal form can be transformed into an implication graph by replacing each of its disjunctions by a pair of implications. For example, the statement ${\displaystyle (x_{0}\lor x_{1})}$ can be rewritten as the pair ${\displaystyle (\neg x_{0}\rightarrow x_{1}),(\neg x_{1}\rightarrow x_{0})}$. An instance is satisfiable if and only if no literal and its negation belong to the same strongly connected component of its implication graph; this characterization can be used to solve 2-satisfiability instances in linear time.^[1]

In CDCL SAT-solvers, unit propagation can be naturally associated with an implication graph that captures all possible ways of deriving all implied literals from decision literals,^[2] which is then used for clause learning.

References