Bounded function

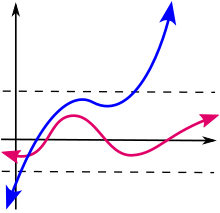
In mathematics, a function ${\displaystyle f}$ defined on some set ${\displaystyle X}$ with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number ${\displaystyle M}$ such that

${\displaystyle |f(x)|\leq M}$

for all ${\displaystyle x}$ in ${\displaystyle X}$.^[1] A function that is not bounded is said to be unbounded.^{[citation needed]}

If ${\displaystyle f}$ is real-valued and ${\displaystyle f(x)\leq A}$ for all ${\displaystyle x}$ in ${\displaystyle X}$, then the function is said to be bounded (from) above by ${\displaystyle A}$. If ${\displaystyle f(x)\geq B}$ for all ${\displaystyle x}$ in ${\displaystyle X}$, then the function is said to be bounded (from) below by ${\displaystyle B}$. A real-valued function is bounded if and only if it is bounded from above and below.^{[1][additional citation(s) needed]}

An important special case is a bounded sequence, where ${\displaystyle X}$ is taken to be the set ${\displaystyle \mathbb {N} }$ of natural numbers. Thus a sequence ${\displaystyle f=(a_{0},a_{1},a_{2},\ldots )}$ is bounded if there exists a real number ${\displaystyle M}$ such that

${\displaystyle |a_{n}|\leq M}$

for every natural number ${\displaystyle n}$. The set of all bounded sequences forms the sequence space ${\displaystyle l^{\infty }}$.^{[citation needed]}

The definition of boundedness can be generalized to functions ${\displaystyle f:X\rightarrow Y}$ taking values in a more general space ${\displaystyle Y}$ by requiring that the image ${\displaystyle f(X)}$ is a bounded set in ${\displaystyle Y}$.^{[citation needed]}

Related notions

Weaker than boundedness is local boundedness. A family of bounded functions may be uniformly bounded.

A bounded operator ${\displaystyle T:X\rightarrow Y}$ is not a bounded function in the sense of this page's definition (unless ${\displaystyle T=0}$), but has the weaker property of preserving boundedness; bounded sets ${\displaystyle M\subseteq X}$ are mapped to bounded sets ${\displaystyle T(M)\subseteq Y}$. This definition can be extended to any function ${\displaystyle f:X\rightarrow Y}$ if ${\displaystyle X}$ and ${\displaystyle Y}$ allow for the concept of a bounded set. Boundedness can also be determined by looking at a graph.^{[citation needed]}

Examples

• The sine function ${\displaystyle \sin :\mathbb {R} \rightarrow \mathbb {R} }$ is bounded since ${\displaystyle |\sin(x)|\leq 1}$ for all ${\displaystyle x\in \mathbb {R} }$.^[1][2]
• The function ${\displaystyle f(x)=(x^{2}-1)^{-1}}$, defined for all real ${\displaystyle x}$ except for −1 and 1, is unbounded. As ${\displaystyle x}$ approaches −1 or 1, the values of this function get larger in magnitude. This function can be made bounded if one restricts its domain to be, for example, ${\displaystyle [2,\infty )}$ or ${\displaystyle (-\infty ,-2]}$.^{[citation needed]}
• The function ${\textstyle f(x)=(x^{2}+1)^{-1}}$, defined for all real ${\displaystyle x}$, is bounded, since ${\textstyle |f(x)|\leq 1}$ for all ${\displaystyle x}$.^{[citation needed]}
• The inverse trigonometric function arctangent defined as: ${\displaystyle y=\arctan(x)}$ or ${\displaystyle x=\tan(y)}$ is increasing for all real numbers ${\displaystyle x}$ and bounded with ${\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}$ radians^[3]
• By the boundedness theorem, every continuous function on a closed interval, such as ${\displaystyle f:[0,1]\rightarrow \mathbb {R} }$, is bounded.^[4] More generally, any continuous function from a compact space into a metric space is bounded.^{[citation needed]}
• All complex-valued functions ${\displaystyle f:\mathbb {C} \rightarrow \mathbb {C} }$ which are entire are either unbounded or constant as a consequence of Liouville's theorem.^[5] In particular, the complex ${\displaystyle \sin :\mathbb {C} \rightarrow \mathbb {C} }$ must be unbounded since it is entire.^{[citation needed]}
• The function ${\displaystyle f}$ which takes the value 0 for ${\displaystyle x}$ rational number and 1 for ${\displaystyle x}$ irrational number (cf. Dirichlet function) is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on ${\displaystyle [0,1]}$ is much larger than the set of continuous functions on that interval.^{[citation needed]} Moreover, continuous functions need not be bounded; for example, the functions ${\displaystyle g:\mathbb {R} ^{2}\to \mathbb {R} }$ and ${\displaystyle h:(0,1)^{2}\to \mathbb {R} }$ defined by ${\displaystyle g(x,y):=x+y}$ and ${\displaystyle h(x,y):={\frac {1}{x+y}}}$ are both continuous, but neither is bounded.^[6] (However, a continuous function must be bounded if its domain is both closed and bounded.^[6])

See also

• Bounded set
• Compact support
• Local boundedness
• Uniform boundedness

References

• v
• t
• e

Lp spaces

Basic concepts

• Banach & Hilbert spaces
• L^p spaces
• Measure
  • Lebesgue
• Measure space
• Measurable space/function
• Minkowski distance
• Sequence spaces

L¹ spaces

• Integrable function
• Lebesgue integration
• Taxicab geometry

L² spaces

• Bessel's
• Cauchy–Schwarz
• Euclidean distance
• Hilbert space
• Parseval's identity
• Polarization identity
• Pythagorean theorem
• Square-integrable function

${\displaystyle L^{\infty }}$ spaces

• Bounded function
• Chebyshev distance
• Infimum and supremum
  • Essential
• Uniform norm

Maps

• Almost everywhere
• Convergence almost everywhere
• Convergence in measure
• Function space
• Integral transform
• Locally integrable function
• Measurable function
• Symmetric decreasing rearrangement

Inequalities

• Babenko–Beckner
• Chebyshev's
• Clarkson's
• Hanner's
• Hausdorff–Young
• Hölder's
• Markov's
• Minkowski
• Young's convolution

Results

• Marcinkiewicz interpolation theorem
• Plancherel theorem
• Riemann–Lebesgue
• Riesz–Fischer theorem
• Riesz–Thorin theorem

For Lebesgue measure	Isoperimetric inequality Brunn–Minkowski theorem Milman's reverse Minkowski–Steiner formula Prékopa–Leindler inequality Vitale's random Brunn–Minkowski inequality

Applications & related

• Bochner space
• Fourier analysis
• Lorentz space
• Probability theory
• Quasinorm
• Real analysis
• Sobolev space
• *-algebra
  • C*-algebra
  • Von Neumann