Acoustic tweezers

Acoustic tweezers (also known as acoustical tweezers) are a set of tools that use sound waves to manipulate the position and movement of very small objects.^[1] Strictly speaking, only a single-beam based configuration can be called acoustical tweezers. However, the broad concept of acoustical tweezers involves two configurations of beams: single beam and standing waves. The technology works by controlling the position of acoustic pressure nodes^[2] that draw objects to specific locations of a standing acoustic field.^[3] The target object must be considerably smaller than the wavelength of sound used, and the technology is typically used to manipulate microscopic particles.^{[citation needed]}

Acoustic waves have been proven safe for biological objects, making them ideal for biomedical applications.^[4] Recently, applications for acoustic tweezers have been found in manipulating sub-millimetre objects, such as flow cytometry, cell separation, cell trapping, single-cell manipulation, and nanomaterial manipulation.^[5] The use of one-dimensional standing waves to manipulate small particles was first reported in the 1982 research article "Ultrasonic Inspection of Fiber Suspensions".^[6]

Method

In a standing acoustic field, objects experience an acoustic-radiation force that moves them to specific regions of the field.^[2] Depending on an object's properties, such as density and compressibility, it can be induced to move to either acoustic pressure nodes (minimum pressure regions) or pressure antinodes (maximum pressure regions).^[3] As a result, by controlling the position of these nodes, the precise movement of objects using sound waves is feasible. Acoustic tweezers do not require expensive equipment or complex experimental setups.^{[citation needed]}

Fundamental theory

Particles in an acoustic field can be moved by forces originating from the interaction among the acoustic waves, fluid, and particles. These forces (including acoustic radiation force, secondary field force between particles, and Stokes drag force) create the phenomena of acoustophoresis, which is the foundation of the acoustic tweezers technology.

Acoustic radiation force

When a particle is suspended in the field of a sound wave, an acoustic radiation force that has risen from the scattering of the acoustic waves is exerted on the particle. This was first modeled and analyzed for incompressible particles in an ideal fluid by Louis King in 1934.^[7] Yosioka and Kawasima calculated the acoustic radiation force on compressible particles in a plane wave field in 1955.^[8] Gorkov summarized the previous work and proposed equations to determine the average force acting on a particle in an arbitrary acoustical field when its size is much smaller than the wavelength of the sound.^[2] Recently, Bruus revisited the problem and gave detailed derivation for the acoustic radiation force.^[9]

As shown in Figure 1, the acoustic radiation force on a small particle results from a non-uniform flux of momentum in the near-field region around the particle, ${\displaystyle \mathbf {\mathit {F^{rad}}} =-\nabla {\mathit {U}}}$, which is caused by the incoming acoustic waves and the scattering on the surface of the particle when acoustic waves propagate through it. For a compressible spherical particle with a diameter much smaller than the wavelength of acoustic waves in an ideal fluid, the acoustic radiation force can be calculated by ${\displaystyle \mathbf {\mathit {F^{rad}}} =-\nabla {\mathit {U}}}$, where ${\displaystyle {\mathit {U}}}$ is a given quantity, also called acoustic potential energy.^[2][9] The acoustic potential energy is expressed as:

${\displaystyle U={V_{0}}({{\overline {p_{in}^{2}}} \over {2{\rho _{f}}c_{f}^{2}}}{f_{1}}-{{3{\rho _{f}}{\overline {v_{in}^{2}}}} \over 4}{f_{2}})}$

where

• ${\displaystyle {\mathit {V_{\mathit {0}}}}}$ is the particle volume,
• ${\displaystyle {\mathit {p_{\mathit {in}}}}}$ is the acoustic pressure,
• ${\displaystyle {\mathit {v_{\mathit {in}}}}}$ is the velocity of acoustic particles,
• ${\displaystyle {\mathit {\rho }}_{\mathit {f}}}$ is the fluid mass density,
• ${\displaystyle {\mathit {c_{\mathit {f}}}}}$ is the speed of sound of the fluid,
• ${\displaystyle {\overline {<*>}}}$ is the time-average term, ${\displaystyle {1 \over T}\int \limits _{0}^{T}{(*)}dt}$

The coefficients ${\displaystyle {\mathit {f_{\mathit {1}}}}}$ and ${\displaystyle {\mathit {f_{\mathit {2}}}}}$ can be calculated by ${\displaystyle {f_{1}}=1-{{{\rho _{f}}c_{f}^{2}} \over {{\rho _{p}}c_{p}^{2}}}}$ and ${\displaystyle {f_{2}}={{2({\rho _{p}}-{\rho _{f}})} \over {2{\rho _{p}}+{\rho _{f}}}}}$

where

• ${\displaystyle {\mathit {\rho }}_{\mathit {p}}}$ is the mass density of the particle,
• ${\displaystyle {\mathit {c}}_{\mathit {p}}}$ is the speed of sound of the particle.

Acoustic radiation force in standing waves

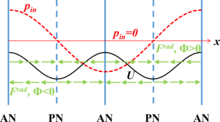
The standing waves can form a stable acoustic potential energy field, so they are able to create stable acoustic radiation force distribution, which is desirable for many acoustic tweezers applications. For one-dimension planar standing waves, the acoustic fields are given by:^[9]

${\displaystyle {A_{in}}(x,t)={{-P_{0}} \over {{\rho _{f}}\omega }}\sin(kx)\sin(\omega t)}$,

${\displaystyle {p_{in}}(x,t)={P_{0}}\cos(kx)\sin(\omega t)}$,

${\displaystyle {\textbf {v}}_{\textbf {in}}(x,t)={\frac {-P_{0}}{\rho _{f}c_{f}}}\sin(kx)\cos(\omega t)){\textbf {e}}_{\textbf {x}}}$,

where

• ${\displaystyle {\mathit {A_{\mathit {in}}}}}$ is the displacement of acoustic particle,
• ${\displaystyle {\mathit {P_{\mathit {0}}}}}$ is the acoustic pressure amplitude,
• ${\displaystyle {\mathit {\omega }}}$ is the angular velocity,
• ${\displaystyle {\mathit {k}}}$ is the wave number.

With these fields, the time-average terms can be obtained. These are:

${\displaystyle {\overline {p_{in}^{2}}}={1 \over 2}P_{0}^{2}{\cos ^{2}}(kx)}$,

${\displaystyle {\overline {v_{in}^{2}}}={{P_{0}^{2}} \over {2\rho _{f}^{2}c_{f}^{2}}}{\sin ^{2}}(kx)}$,

Thus, the acoustic potential energy is:

${\displaystyle U={V_{0}}{{P_{0}^{2}} \over {4{\rho _{f}}c_{f}^{2}}}[{\cos ^{2}}(kx){f_{1}}-{3 \over 2}{\sin ^{2}}(kx){f_{2}}]}$,

Then, the acoustic radiation force is found by differentiation:

${\displaystyle {F_{x}}^{rad}=-{\partial _{x}}U={V_{0}}k{E_{ac}}\sin(2kx)\Phi }$,

${\displaystyle {E_{ac}}={{P_{0}^{2}} \over {4{\rho _{f}}c_{f}^{2}}}}$, ${\displaystyle \Phi ={f_{1}}+{3 \over 2}{f_{2}}={{5{\rho _{p}}-2{\rho _{f}}} \over {2{\rho _{p}}+{\rho _{f}}}}-{{{\rho _{f}}c_{f}^{2}} \over {{\rho _{p}}c_{p}^{2}}}}$,

where

• ${\displaystyle {\mathit {E_{\mathit {ac}}}}}$ is the acoustic energy density, and
• ${\displaystyle \Phi }$ is acoustophoretic contrast factor.

The term ${\displaystyle \sin({\mathit {2kx}})}$ shows that the radiation force period is one-half of the pressure period. Also, the contrast factor can be positive or negative depending on the properties of particles and fluid. For positive value of ${\displaystyle \Phi }$, the radiation force points from the pressure antinodes to the pressure nodes, as shown in Figure 2, and the particles will be pushed to the pressure nodes.

Secondary acoustic forces

When multiple particles in a suspension are exposed to a standing wave field, they will not only experience acoustic radiation force, but also secondary acoustic forces caused by waves scattered by other particles. The inter-particle forces are sometimes called Bjerknes forces. A simplified equation for the inter-particle forces of identical particles is:^[10][11]

${\displaystyle {F_{B}}(x)=4\pi {a^{6}}[{{{{({\rho _{p}}-{\rho _{f}})}^{2}}(3{{\cos }^{2}}\theta -1)} \over {6{\rho _{f}}{d^{4}}}}{v_{in}}^{2}(x)-{{\omega ^{2}{\rho _{f}}} \over {9{d^{2}}}}{({1 \over {{\rho _{p}}c_{p}^{2}}}-{1 \over {{\rho _{f}}c_{f}^{2}}})^{2}}p_{in}^{2}(x)]}$

where

• ${\displaystyle {\mathit {a}}}$ is the radius of the particle,
• ${\displaystyle {\mathit {d}}}$ is the distance between the particles,
• ${\displaystyle {\mathit {\theta }}}$ is the angle between the central line of the particles and the direction of propagation of the incident acoustic wave.

The sign of the force represents its direction: a negative sign for an attractive force, and a positive sign for a repulsive force. The left side of the equation depends on the acoustic particle velocity amplitude ${\displaystyle {\mathit {v}}_{\mathit {in}}({\mathit {x}})}$ and the right side depends on the acoustic pressure amplitude ${\displaystyle {\mathit {p}}_{\mathit {in}}({\mathit {x}})}$. The velocity-dependent term is repulsive when particles are aligned with wave propagation (Θ=0°), and negative when perpendicular to wave propagation (Θ=90°). The pressure-dependent term is unaffected by the particle orientation and is always attractive. In the case of a positive contrast factor, the velocity-dependent term diminishes as particles are driven to the velocity node (pressure antinode), as in the case of air bubbles and lipid vesicles. In a similar way, the pressure-dependent term diminishes as particles are driven towards the pressure node (velocity antinode), as are most solid particles in aqueous solutions.

In addition to the scattering-related secondary acoustic forces, the flow field resulting from the interactions of the various acoustic streaming fields, generated by the acoustic boundary layer of each particle (sometimes called microstreaming), can induce additional viscous shear forces on each of the particles' surfaces, which then results in an additional contribution to the secondary acoustic forces in its fully viscous formulations.^[12] The viscous effects on the secondary acoustic force can become significant when compared to the perfect fluid formulation exemplified above, and even dominant in certain limit cases, yielding both quantitatively and qualitatively different results than what is predicted by inviscid theory.^[13] The relevance of the viscous contributions varies greatly depending on the specific case being investigated, and thus important care needs to be taken in selecting an appropriate secondary acoustic force model for the given scenario.

The influence of the secondary forces is usually very weak, and only has an effect when the distance between particles is very small. It becomes important in aggregation and sedimentation applications, where particles are initially gathered in nodes by the acoustic radiation force. As inter-particle distances become smaller, the secondary forces assist in further aggregation until the clusters become heavy enough for sedimentation to begin.

Acoustic streaming

Acoustic streaming is a steady flow generated by the nonlinear component of the oscillations in an acoustic field.^{[further explanation needed]} Depending on the mechanisms, the acoustic streaming can be categorized into two general types, Eckart streaming and Rayleigh streaming.^[14][15] Eckart streaming is driven by a time-average momentum flux created when high-amplitude acoustic waves propagate and attenuate in a fluid. Rayleigh streaming, also called "boundary driven streaming", is forced by Reynolds stresses in the viscous boundary layer. Both of the driven mechanisms come from a time-average nonlinear effect.

A perturbation approach is used to analyze the phenomenon of nonlinear acoustic streaming.^[16] The governing equations for this problem are mass conservation and Navier-Stokes equations：

${\displaystyle \partial _{\mathit {t}}{\mathit {\rho }}=-\nabla \cdot ({\mathit {\rho }}{\textbf {v}})}$,

${\displaystyle {\mathit {\rho }}[\partial _{\mathit {t}}{\textbf {v}}+({\textbf {v}}\cdot \nabla ){\textbf {v}}]=-\nabla {\mathit {p}}+{\mathit {\mu }}\nabla ^{2}{\textbf {v}}+{\mathit {\beta }}{\mathit {\mu }}\nabla (\nabla \cdot {\textbf {v}}))}$

where

• ${\displaystyle {\mathit {\rho }}}$ is the density of fluid,
• ${\displaystyle {\textbf {v}}}$ is the velocity of fluid particle,
• ${\displaystyle {\mathit {p}}}$ is the pressure,
• ${\displaystyle {\mathit {\mu }}}$ is the dynamic viscosity of fluid,
• ${\displaystyle {\mathit {\beta }}}$ is the viscosity ratio.

The perturbation series can be written as ${\displaystyle p={p_{0}}+{p_{1}}+{p_{2}}}$, ${\displaystyle {\textbf {v}}={\textbf {0}}+{\textbf {v}}_{\textbf {1}}+{\textbf {v}}_{\textbf {2}}}$, ${\displaystyle {\mathit {\rho }}={\mathit {\rho }}_{0}+{\mathit {\rho }}_{1}+{\mathit {\rho }}_{2}}$, which are diminishing series with the higher-order terms much smaller than the lower-order ones.

The liquid is quiescent and homogeneous at its zero-order state. Substituting the perturbation series into the mass conservation and Navier-Stokes equation and using the relation of ${\displaystyle {p_{1}}=c_{f}^{2}{\rho _{1}}}$, the first-order equations can be obtained by collecting terms in first-order,

${\displaystyle \partial _{\mathit {t}}{\mathit {p}}_{1}=-{\mathit {\rho }}_{0}{\mathit {c}}_{\mathit {f}}^{2}\nabla \cdot {\textbf {v}}_{\textbf {1}}}$,

${\displaystyle {\mathit {\rho }}_{0}\partial _{\mathit {t}}{\textbf {v}}_{\textbf {1}}=-\nabla {\mathit {p}}_{1}+{\mathit {\mu }}\nabla ^{2}{\textbf {v}}_{\textbf {1}}+{\mathit {\beta }}{\mathit {\mu }}\nabla (\nabla \cdot {\textbf {v}}_{\textbf {1}})}$.

Similarly, the second-order equations can be found as well,

${\displaystyle \partial _{\mathit {t}}{\mathit {\rho }}_{2}=-{\mathit {\rho }}_{0}\nabla \cdot {\textbf {v}}_{\textbf {2}}-\nabla \cdot ({\mathit {\rho }}_{1}{\textbf {v}}_{\textbf {1}})}$,

${\displaystyle {\mathit {\rho }}_{0}\partial _{\mathit {t}}{\textbf {v}}_{\textbf {2}}=-\nabla {\mathit {p}}_{2}+{\mathit {\mu }}\nabla ^{2}{\textbf {v}}_{\textbf {2}}+{\mathit {\beta }}{\mathit {\mu }}\nabla (\nabla \cdot {\textbf {v}}_{\textbf {2}})-{\mathit {\rho }}_{1}\partial _{t}{\textbf {v}}_{\textbf {1}}-{\mathit {\rho }}_{0}({\textbf {v}}_{\textbf {1}}\cdot \nabla ){\textbf {v}}_{\textbf {1}}}$.

For the first-order equations, taking the time derivation of the Navier-Stokes equation and inserting the mass conservation, a combined equation can be found:

${\displaystyle {1 \over {c_{f}^{2}}}\partial _{t}^{2}{p_{1}}=[1-{{(1-\beta )\mu } \over {{\rho _{0}}c_{f}^{2}}}{\partial _{t}}]{\nabla ^{2}}{p_{1}}}$.

This is an acoustic wave equation with viscous attenuation. Physically, ${\displaystyle {\mathit {p}}_{1}}$ and ${\displaystyle {\textbf {v}}_{\textbf {1}}}$ can be interpreted as the acoustic pressure and the velocity of the acoustic particle.

The second-order equations can be considered as governing equations used to describe the motion of fluid with mass source ${\displaystyle [-\nabla \cdot ({\mathit {\rho }}_{1}{\textbf {v}}_{\textbf {1}}))]}$ and force source ${\displaystyle [-\rho _{1}\partial _{t}{\textbf {v}}_{\textbf {1}}-\rho _{0}({\textbf {v}}_{\textbf {1}}\cdot \nabla ){\textbf {v}}_{\textbf {1}}]}$. Generally, the acoustic streaming is a steady mean flow, where the response time scale is much smaller than the one of the acoustic vibration. The time-average term ${\displaystyle {\overline {{\textbf {v}}_{\textbf {2}}}}}$ is normally used to present the acoustic streaming. By using ${\displaystyle {\overline {\partial _{\mathit {t}}{\mathit {\rho }}_{2}}}=0}$, the time-average second-order equations can be obtained:

${\displaystyle {\mathit {\rho }}_{0}\nabla \cdot {\overline {{\textbf {v}}_{\textbf {2}}}}=-\nabla \cdot {\overline {({\mathit {\rho }}_{1}{\textbf {v}}_{\textbf {1}})}}}$,

${\displaystyle {\mathit {\mu }}\nabla ^{2}{\overline {{\textbf {v}}_{\textbf {2}}}}+{\mathit {\beta }}{\mathit {\mu }}\nabla (\nabla \cdot {\overline {{\textbf {v}}_{\textbf {2}}}})-{\overline {\nabla {\mathit {p}}_{2}}}={\overline {{\mathit {\rho }}_{1}\partial _{\mathit {t}}{\textbf {v}}_{\textbf {1}}}}-{\mathit {\rho }}_{0}{\overline {({\textbf {v}}_{\textbf {1}}\cdot \nabla ){\textbf {v}}_{\textbf {1}}}}}$.

It is important to note that the time-averaging of pure first-order terms lead to their cancellation, since they are by definition harmonic. This means that they are pure sine waves, and thus have a mean of 0, which leads to the cancellation of any term that contains them. Second-order terms are, however, not harmonic, and do not get cancelled out by time-averaging.^[17] This is most important for understanding acoustic streaming: first-order terms, related to simple oscillatory motion, have much larger magnitudes than second-order terms, and thus are dominant in the oscillation time-scale. Those first-order terms, however, being pure sines, in a quasi-steady state, repeat after each oscillation cycle, yielding no net fluid flow. Second-order terms, instead, are not harmonic, and thus can have a cumulative effect which, despite being smaller, can add up over many oscillation cycles, leading to the development of the net steady-state flow we identify as acoustic streaming.

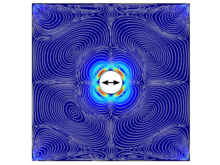
In determining the acoustic streaming, the second-order equations are thus most important. Since Navier-Stokes equations can only be analytically solved for simple cases, numerical methods are typically used, with the finite element method (FEM) the most common technique. It can be employed to simulate the acoustic streaming phenomena. Figure 3 is one example of acoustic streaming around a solid circular pillar, which is calculated by FEM.

As mentioned, acoustic streaming is driven by mass and force sources originating from the acoustic attenuation. However, these are not the only driven forces for acoustic streaming. The boundary vibration may also contribute, especially to "boundary driven streaming". For these cases, the boundary condition should also be processed by the perturbation approach and be imposed on the two order equations accordingly.

Particle motion

The motion of a suspended particle whose gravity is balanced by the buoyancy force in an acoustic field is determined by two forces: the acoustic radiation force and Stokes drag force. By applying Newton's law, the motion can be described as:

${\displaystyle {\mathit {m}}{\frac {d{\textit {u}}}{\mathit {dt}}}={\textit {F}}^{\textit {rad}}+{\textit {F}}^{\textit {drag}}}$,

${\displaystyle {\textit {F}}^{\textit {drag}}=6\pi {\mathit {a}}{\mathit {\mu }}({\textit {v}}-{\textit {u}})}$.

where

• ${\displaystyle {\textit {v}}}$ is the fluid velocity,
• ${\displaystyle {\textit {u}}}$ is the velocity of particle.

For applications in a static flow, the fluid velocity comes from the acoustic streaming. The magnitude of acoustic streaming depends on the power and frequency of the input and the properties of the fluid media. For typical acoustic-based microdevices, the operating frequency may be from the kHz to the MHz range. The vibration amplitude is in a range of 0.1 nm to 1 μm. Assuming the fluid used is water, the estimated magnitude of acoustic streaming is in the range of 1 μm/s to 1 mm/s. Thus, the acoustic streaming should be smaller than the main flow for most continuous flow applications. The drag force is mainly induced by the main flow in those applications.

Applications